I'm starting rubber ducking, BCM rule and LTP

Last updated on Feb 23, 2025

I only took one coding class and it didn't teach me much in terms of hard skills, or soft skills really, but it did leave me with the idea of 'rubber ducking', explaining a problem and your approach so far to an inanimate object in hopes of seeing a solution or flaw in your previous steps. That's kind of what I'm doing here. Currently, I am trying to get the BCM rule or something similar to recreate the dynamics of LTP and LTD simultaneously. I'm sure someone already has done this but hey you don't learn if you don't do. That said if this takes much longer I hope I look for a paper doing just what I am. I was very ambitions trying to jump straight from learning rule to learning an actual task. Perhaps I should instead see if I can recreate the simplest possible thing, response to one single stimulus. Turns out that's actually quite hard even though it sounds easy. Specifically, I am trying to recreate these plots:

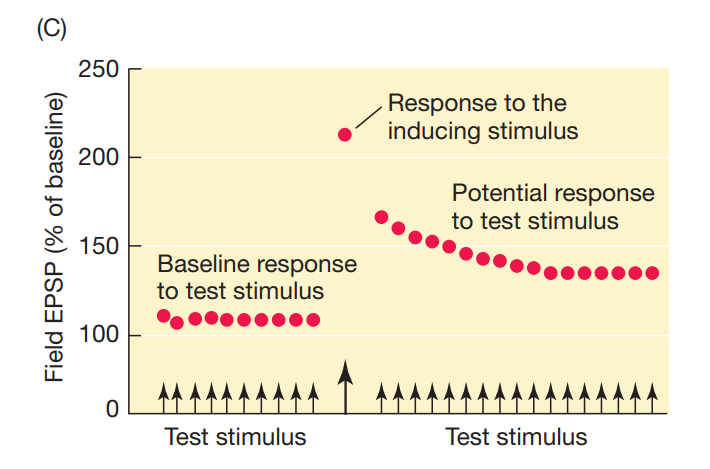
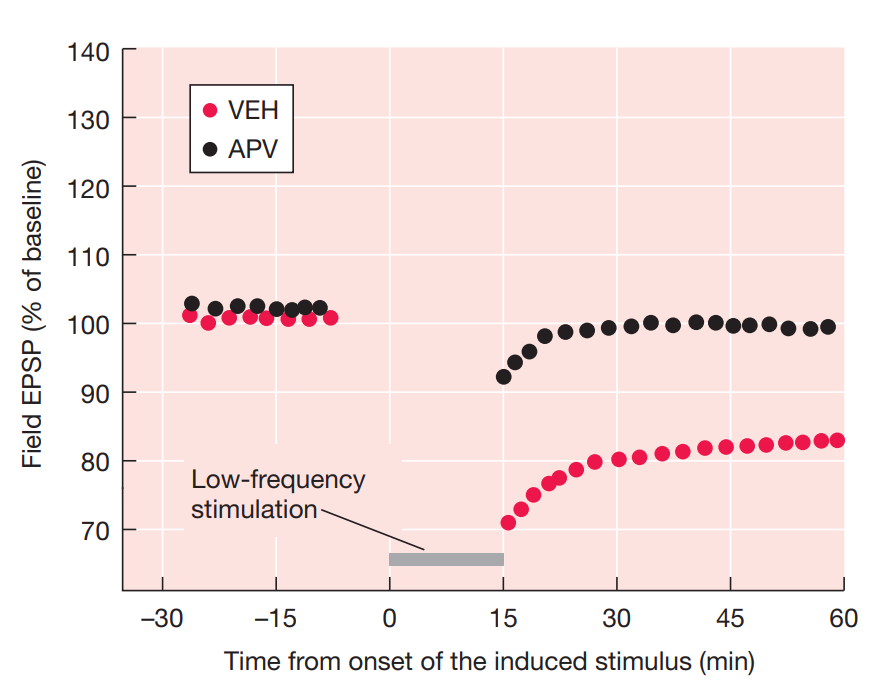
from the textbook Neurobiology of Learning and Memory using the BCM rule from this paper https://www.jneurosci.org/content/jneuro/2/1/32.full.pdf. I also added an exponential decay to the BCM rule to keep if from going off to extrema. Problem is that apparently causes it to oscillate relentlessly.

The first part is just getting stable activity in response to stable stimuli. I haven't gotten this yet. Maybe I should try more neurons or (hey an idea I had while writing this, rubber ducking may be working) but more likely I will have to modify the learning rules in some way. I could cheat and have the learning rate decay but then I wouldn't have any way to learn. Which yes is very obvious but I don't have really great ideas on how to damp oscillations. Here are some images of what I'm dealing with just as reference.

Average firing rate in Hz over 1000 seconds of pretty much the same input Synaptic weights update every second

From now on, I'm going to start accompanying these with specific commits of the code. Maybe someday taking notes will actually help me. I tried looking at what happens when there is no decay. It still kind of oscillates. I have an artificailly imposed maximumsynaptic weight (3 times the starting mean) and I think what happens is a bunch of neurons get there and then they lower again from bcm rule as the average firing rate increases. Here is an image:

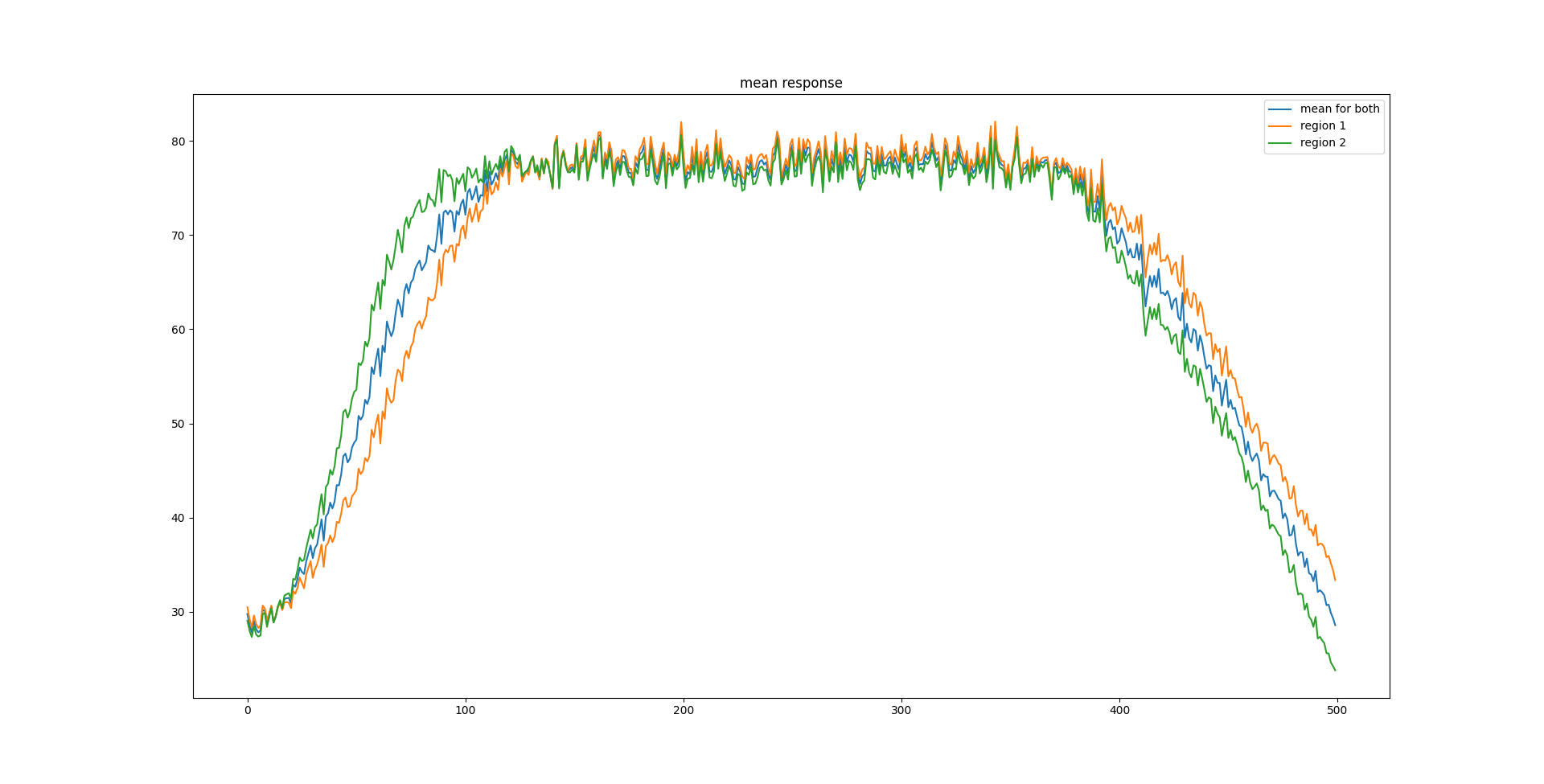
Whatever the case, it clearly isn't stable for a stable input so there needs to be some homeostatic mechanism. Actually maybe not? The BCM paper mentions stable and unstable points of attraction.

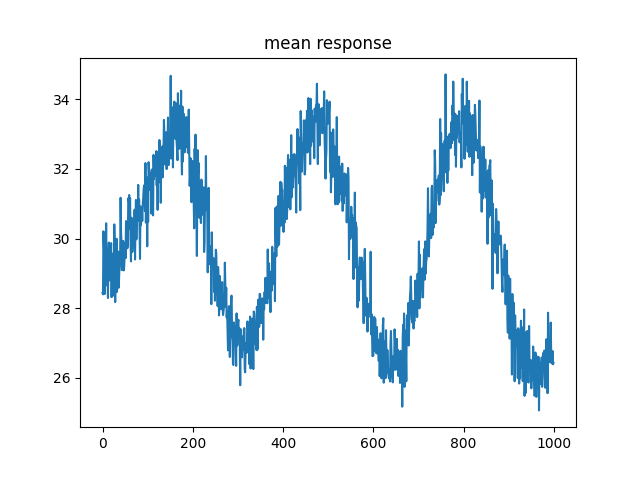
I never actually came back to do this because my oscillations were from the buffer thing, could still be cool to make

Let's see if I can't recreate that plot at least. Unsirprisingly, just having the decay term gives oscillations in the mean response, probably because I am basically using the equation of spring.

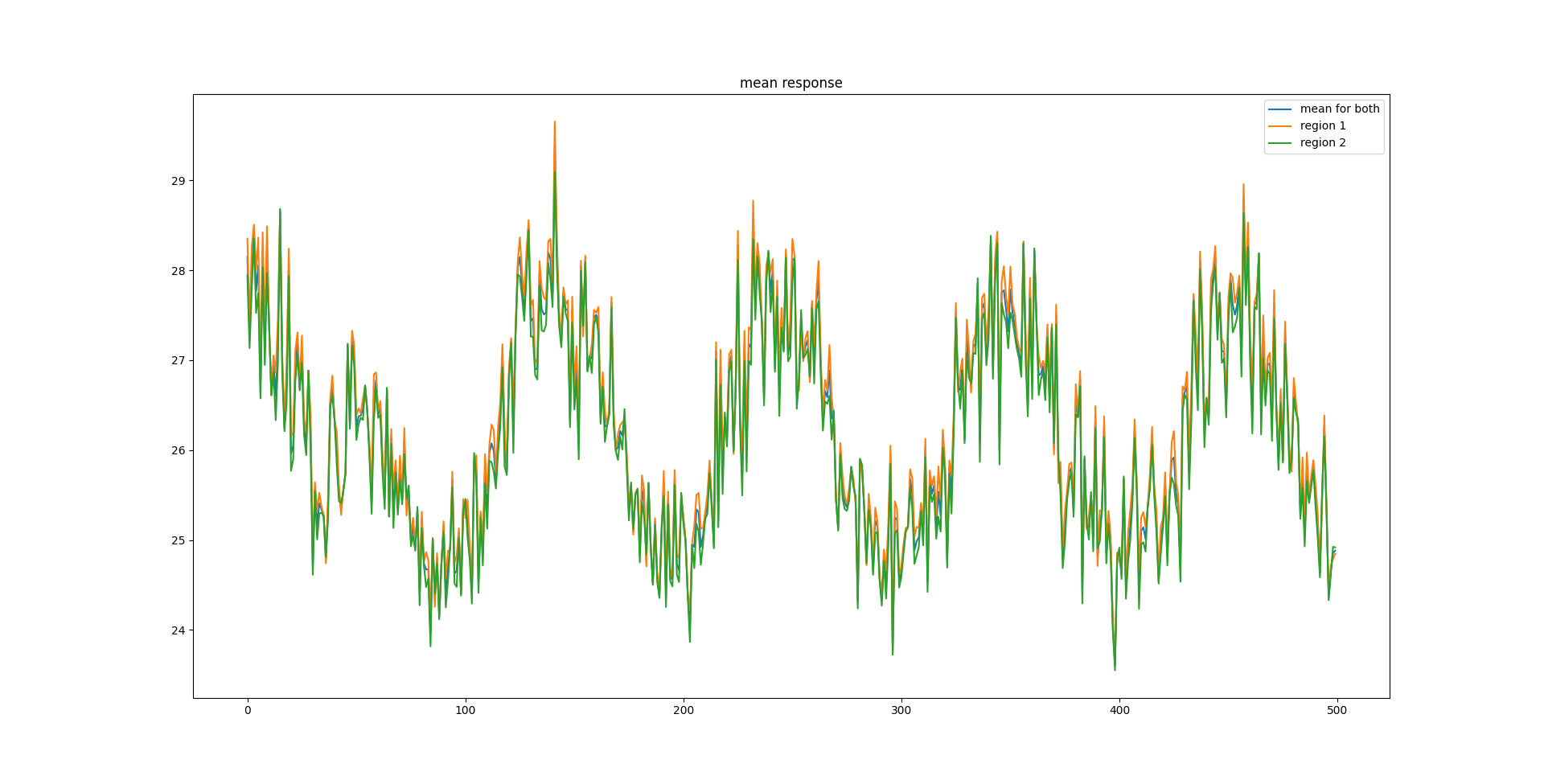
Mean response (firing rate Hz) to stimulus over 500 seconds, synapses updated by the second

Code for the synaptic weight update function. Astute readers may ask why this function is named cherry_pie, that is simply because I was in a flow state listening to Cherry Pie by Warrant on repeat as I coded it

Actually, I take that back, this should not oscillate, I have no analog to momentum. I am genuinely confused right now. Probably because I am stupid. Yep I'm dumb as a box of rocks. So I have a variable called buffer_del_syn_weights and I added the weight change to it because it was meant to be for batching but I'm not doing batching, anyway that gives the oscillations because I'm dumb and never zerod it out.

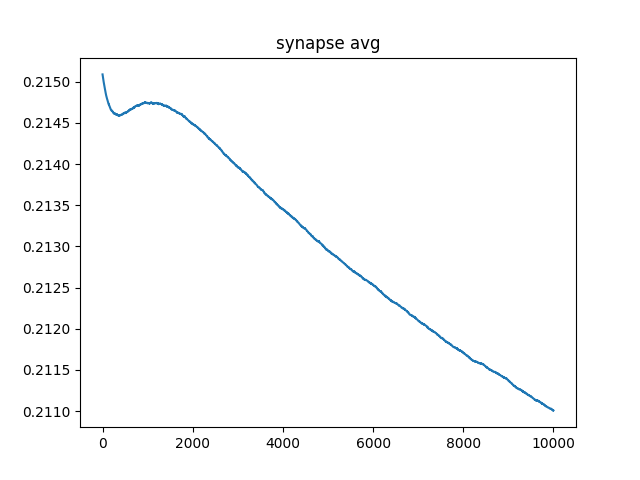
So that's with BCM + the decay being actually fixed, it looks like it might still be oscillating which would make me sad. I am going to run for much longer and report. Oh and it doens't oscillate when I don't have the BCM acting, at least it doens't look like it, see below.

Hey I'm just writing here to make it clear this is for the very long run to see if there are still oscillations.

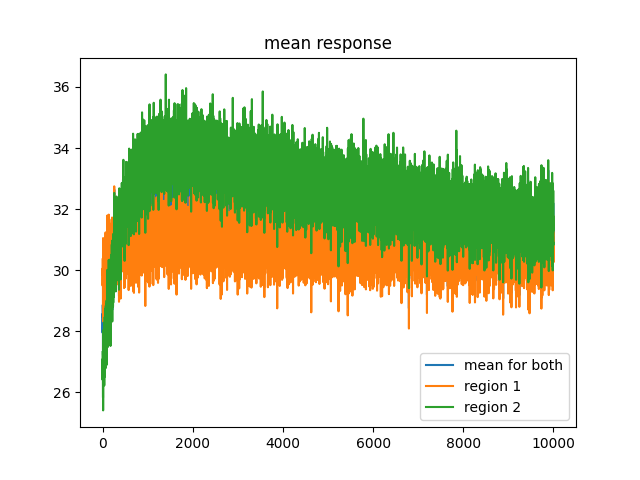
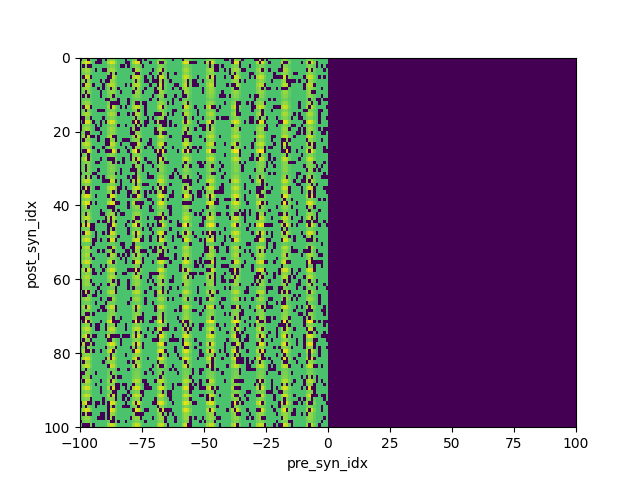
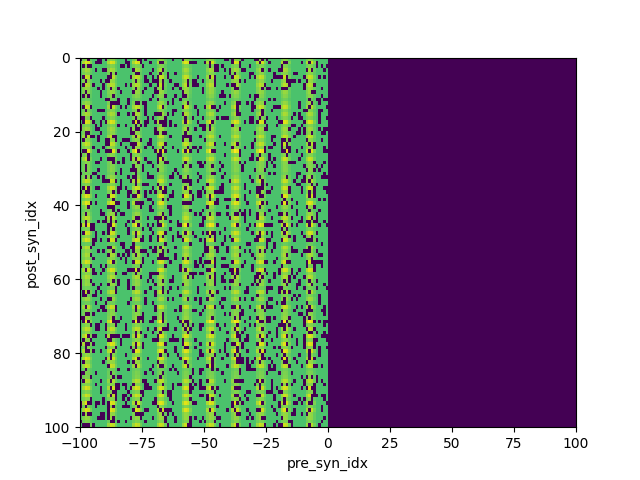
So yeah it worked that's pretty cool, you can even see the spatial frequency stuff directly imprint on the synapses, those are the vertical stripes. I'm going to try to actually train it to recognize the difference between horizontal and vertical spatial oscillations and see if that works.

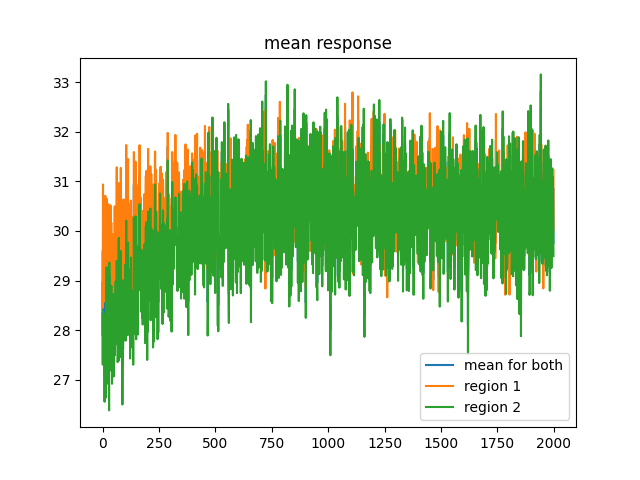
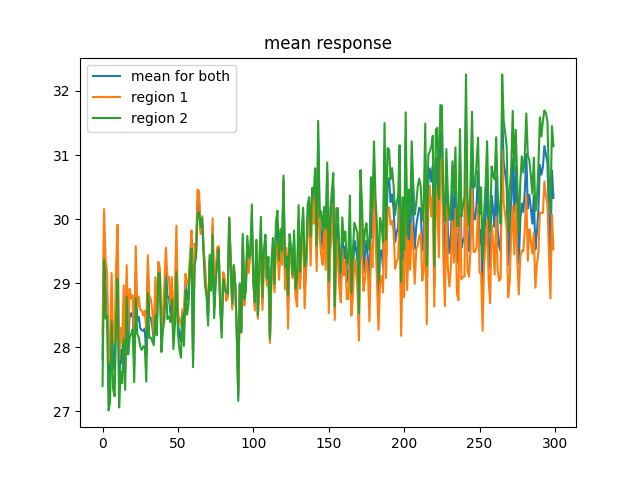
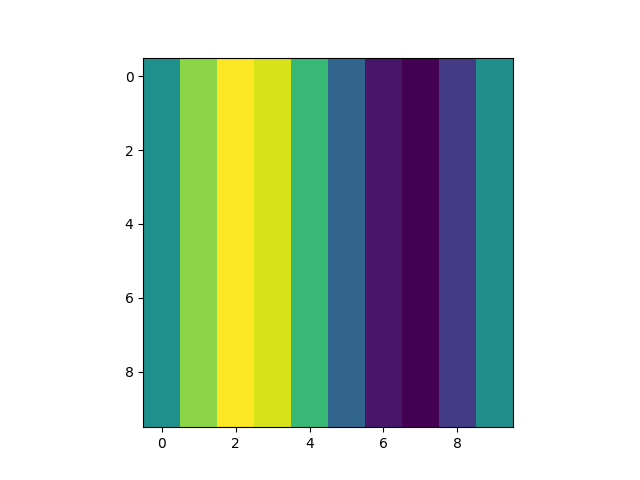
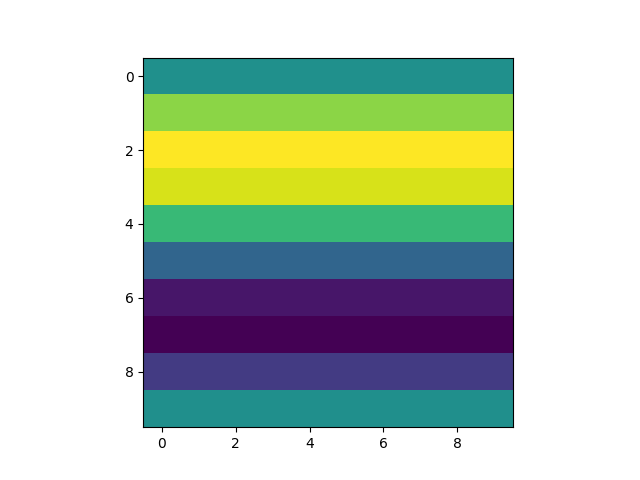
Folks as you can plainly see, each region (really it should be population) has approximately equal response on average. However, this is actually literally perfect at distinguishing the two patterns so hey that's cool. Um here are the images of the two patterns and here is the code to test that. There are 100 input neurons so these 10x10 grids represent the stimulus strength for those neurons.

Ok so this is cool but let's not lose sight of my main goal, to see if this BCM stuff can recreate those LTP and LTD curves. Also while I'm here I might be able to get this to do mnist recognition and noise stuff but let's not get hasty. Oh I also want to see if this can generalize to multilayer systems or an architecture with feedback or for time varying data, but again one thing at a time. I have shown that this rule can result in at least some selectivity, but can it do that after literally one second of higher stimulus with a given pattern?

It has come to my attention I didn't actually explain how training works or really what BCM is. The training basically artificially halves the firing rate of the neurons we want to not be active for a given pattern and does nothing to the others. The BCM rule looks like this:

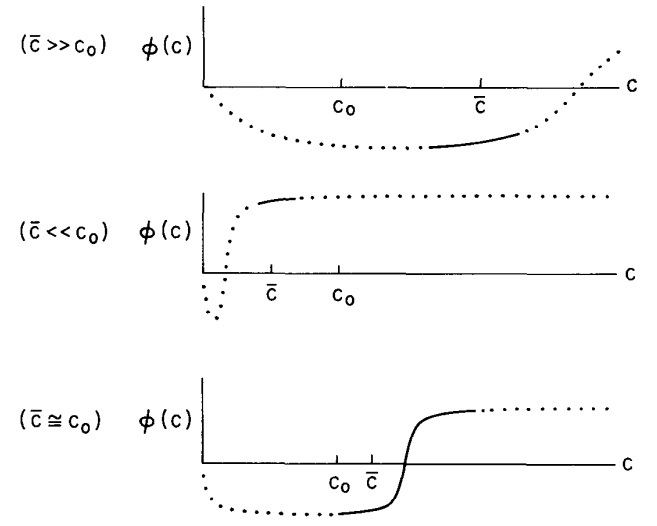
C is the firing rate of the post-synaptic neuron, C0 is some tunable constant, C bar is the average firing rate. For this to be the true BCM rule it would be multiplied by the pre-synaptic neuron activity but that would not change the shape of the graph. Play around in desmos: https://www.desmos.com/calculator/wriw5fmx6b

So, the neurons with lower than average firing rates have their weights depressed and that generates the selectivity to specific patterns.

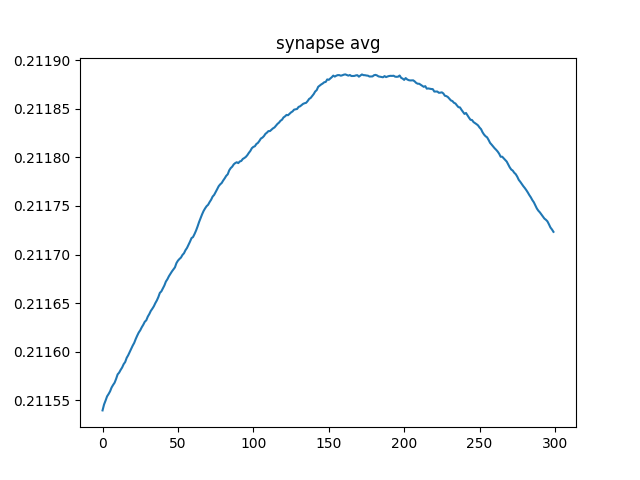
Anyway, here is what happens if you have one second of elevated stimulus with the same learning rules:

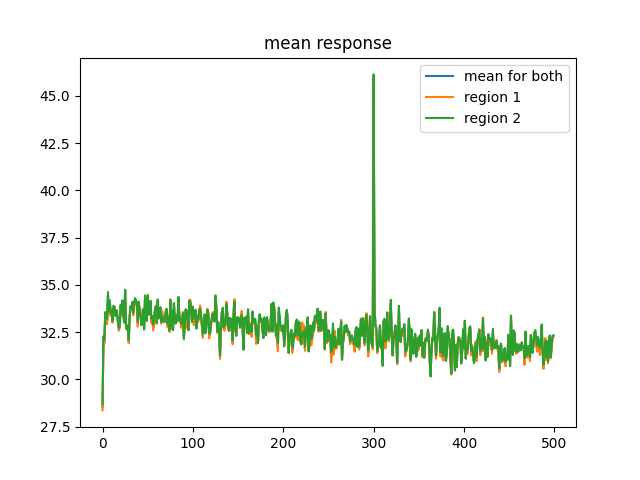
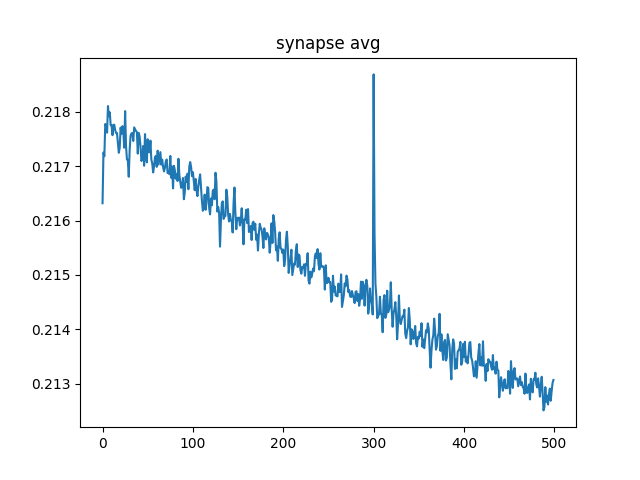
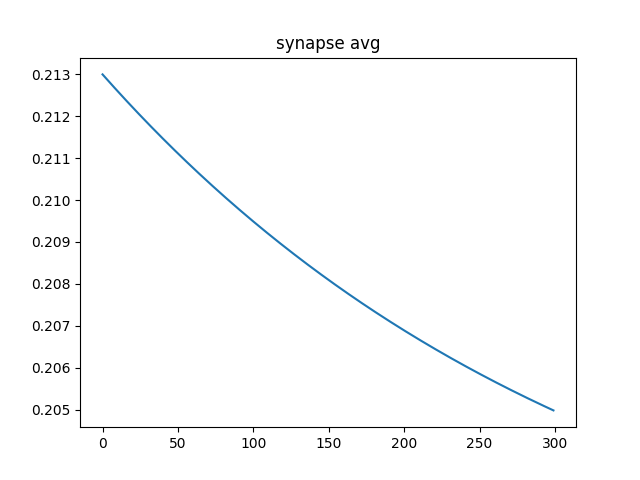
As you can see this was simulated for 500 seconds, much longer than should be necessary but I wanted to make sure things were at least slightly stable. I can see that it is still decaying but it is by 0.005 over the course of 500 seconds which I find acceptable. Oh and this is with the learning rate of 25, it was 0.1 for geting the slectivity generated so yeah, not reporducing LTP even with huge learning signal. Maybe the decay is too strong? I will decrease and try.

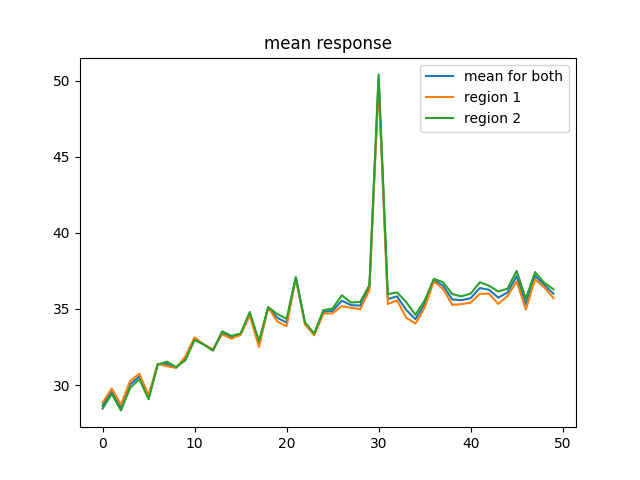
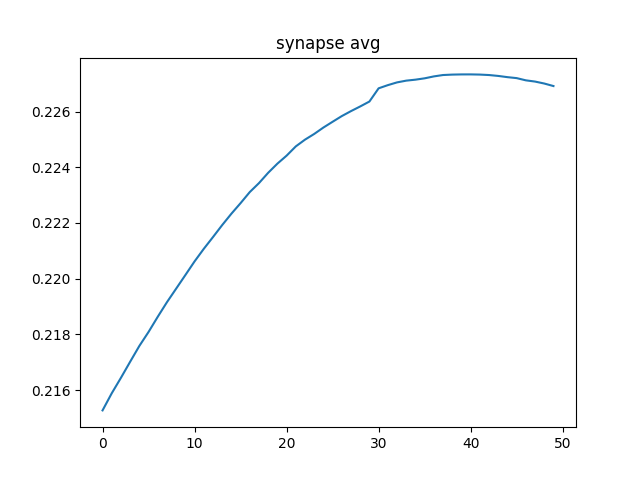
That is with the BCM rule 2x it's previous strength relative to the decay. Clearly that was not the issue. I am filled with a deep sadness. I will keep trying this but it seems that BCM, in some circumstances, is capable of learning real patterns but not capable of recreating the relatively simple dynamics of LTP. Again, I will keep working and it's quite possible this is on me but like, come on man. Can't I get a learning rule that does it all? Although that does beg the question, is there one learning rule that governs everything? There could be like a million that all have different relative strengths in different regions or times. That would really suck.