To Spiking Neurons

The road to simulating spiking neurons was not an easy one. Information on the more traditional forms of artificial neural networks is easier to find and implement, at least for me. To make the neural networks in the first part of this project, it was basically matrix multiplication. The code was brief and only really needed NumPy to function. This is not the case for biological neuron models. I went with perhaps the simplest model, the Izhikevich model which you can read the original paper on here. There are other models I won't discuss as to not do them a disservice. I'm not a neuroscientist so everything I know is self taught. I think I can do justice to the Izhikevich model since I understand it well enough to code it but if you're interested in others, look elsewhere. But how exactly did I implement them? That will be the focus of this post with a brief aside to talk about what is a much more full fledged package for doing this sort of thing.

Because I have no formal experience with neuroscience, I thought it best to use existing packages to circumvent my inexperience. This wasn't a bad plan but I should have known better. I have an admittedly bad habit of making my own code instead of doubling down to understand someone else's. What I tried to use was called NeuroML which can be read about in great detail here. It has everything I needed and then some. In fact, its good enough to have been used in serious scientific investigations. The issue was that it was just too much for me to use and I'm impatient. It saved and loaded all the models and all the data each run which greatly increased the amount of time to run for even a very short simulation. It had what I considered to be an unintuitive method of building the actual networks. Some of the example code on the site didn't work when I tried to run it which is always frustrating. I have no doubt that if I stuck with it, it would have been great for my purposes. But since I only need the Izhikevich model I just implemented that from scratch and ignored the rest. Some day I'll likely come back to NeuroML, but I needed to make progress on my project, not understanding someone else's.

Perhaps I should explain how spiking neurons are different from the kind of neurons used previously in more detail. As I've already said, they exhibit time varying behavior. A constant input current will yield a time varying voltage of the neuron. They are called spiking because the voltage will very quickly increase then fall back down which look like spikes when plotted against time. Previously, the input signal would set the neuron value and this would propagate down the line giving each neuron a fixed value for a fixed input. This brings me to a second difference. The signal takes time to propagate. The current the pre-synaptic neuron is feeding to the post-synaptic neuron is only updated every millisecond. So for a few milliseconds at the start of the signaling, the output neurons have no information on what the input even is. A question you may be asking is "How do we even know what the output should be if the voltage is constantly changing?". I counted the number of spikes, or firing events, in a certain length of time during which the input signal was supplied. Whichever output neuron had the most spikes was considered the choice of the neural network. This method works well for classification as I am still using the iris dataset from the last part of this project.

Well, I've mentioned the Izhikevich model several times now, but what is it and why is it so attractive to me? Essentially, it is a model of spiking neurons that only requires two differential equations to display all sorts of very accurate behavior. This is good for two reasons. The first is that its simple enough to understand without a lot of background neuroscience or biology knowledge. You can tie it to information on ion channels and neurotransmitters but I don't need to know the intricacies of the real biology to implement and understand the math. The other benefit is more pragmatic. Because it is so simple, many neurons can be simulated with relatively small amounts of computing power. I only have a few dozen neurons in my model but I'm still glad about its efficiency. The models I'm using can be simulated in nearly real time with millisecond precision without any parallelization and in python which is great because I'm simulation many of them for thousands of seconds each. Doing a rewrite in a lower level language and parallelizing could make this run faster than real time with relatively modest hardware. Hopefully this is sufficient justification for why this model was selected and now I can get into the actual math.

I will do my best to describe the math, but the paper is really quite brief and very readable as far as academic papers are concerned. Anyway, there are two variables of particular interest. The first is voltage, "v", of the cell membrane and the other is "u" which is unitless and is a recovery variable that provides negative feedback on voltage. The differential equation for "v" is given by 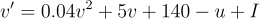while "u" is given by 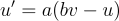. Additionally, whenever the neuron spikes, as defined by voltage being greater than 30mV, "v" and "u" are reset by 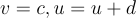. 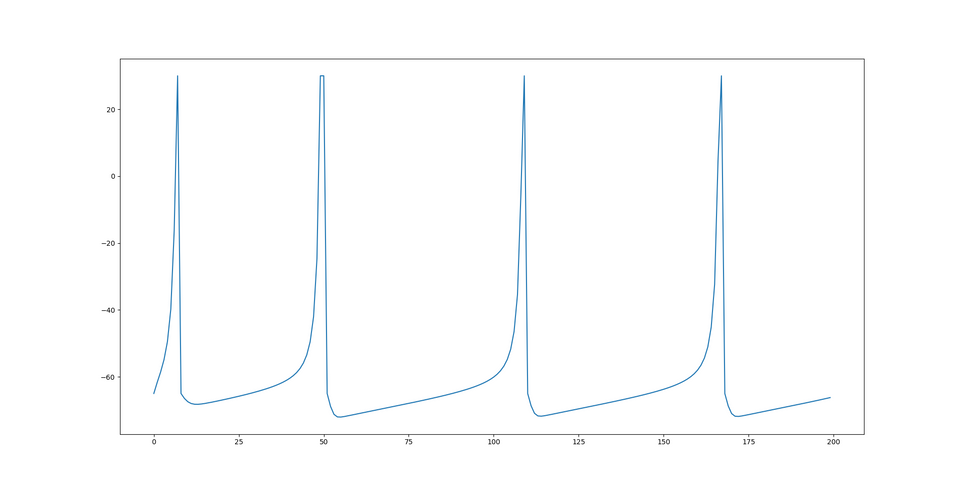You may be wondering what all the constants, "a", "b", "c", and "d" are. They are all dimensionless quantities used to curve fit to measured neural activity. By changing them, the spiking patterns change as different cell types exhibit different behavior. When initializing a model, each neuron is set to 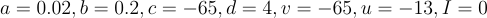which gives pretty average values for the dimensionless quantities. None of this has touched on the synapse model which is also integral to changing the network's behavior and is what is actually varied. I will discuss that next. Here is an image of the spiking behavior generated by this model:

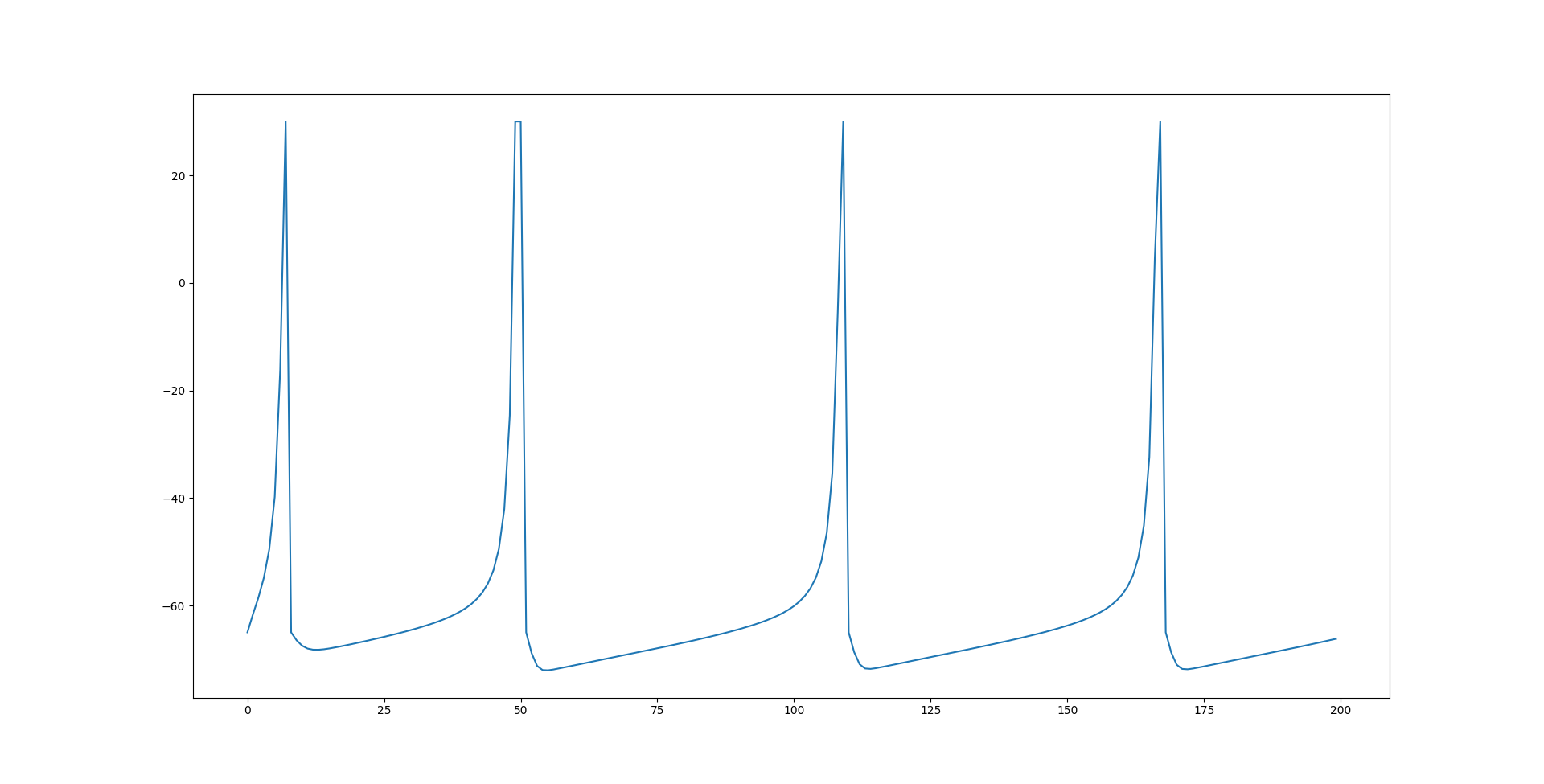
I may be misunderstanding the synapse model used in the original paper but when I implemented it I had poor results. I actually tried to copy the synapse model used in NeuroML but either they have very poor documentation or I was looking in the wrong place. The model I ended up using is likley the same, but I don't know exactly what they used so I can't say for sure. What I ended up using was a model partially explained to me by ChatGPT. It has two factors, gbase and tau which correspond to conductance and a time decay constant respectively. When the voltage of a pre-synaptic neuron crosses some threshold a timer starts and the neuron begins conducting. As time goes on, the conductance of the neuron decreases until there it is essentially back to zero. Currently can only flow from pre to post-synaptic neurons and a pre-synaptic neuron at a lower membrane voltage will still increase the current going into a post-synaptic neuron. Additionally, inhibitory neurons will decrease the current going into their post-synaptic neuronns. The equations used for the current from a synapse of an excitatory neuron is 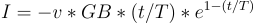while an inhibitory neuron uses 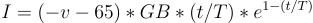. One may argue that there should be considerations of neurotransmitters rather than currents exclusively. That is probably true but also not a consideration that needs to be made to have seemingly accurate behavior. Now, I think my implementation is still a little wrong, or at least has room for improvement. But it does contain essentially everything I am interested, spiking behavior with non linear functions but not just reducing it to the point of binary spikes of on and off. The below graph shows some imperfect spiking behavior of a neuron at the end of the network with the described synapse model connecting neurons to each other.

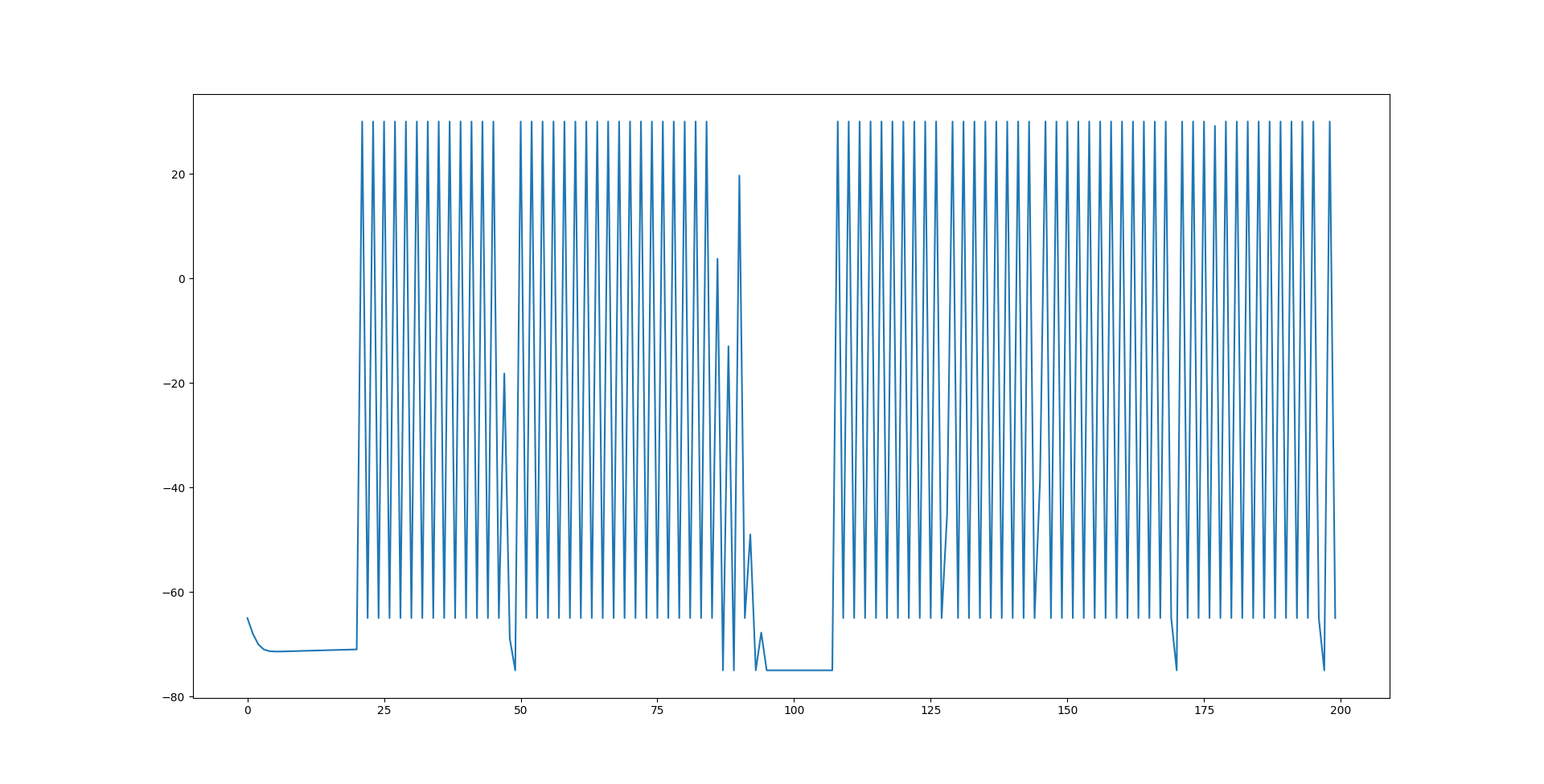
And that's everything. I was intending to have information on training these networks, but I think my current method is not working as well as I thought and I know it isn't optimal. As such, a dedicated post will be given for that once I get acceptable accuracy on classifying the iris dataset. I may try and do the synaptic weight recreation on random models as my original goal isn't training neuromorphic AI, but it certainly is interesting.