A Vastly Improved Implementation of the Izhikevich Neuron Model

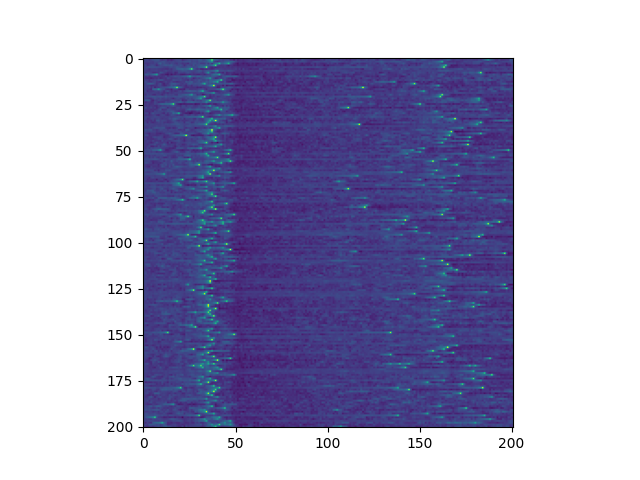
I did a final project for a biophysics class that involved this neuron model and I grew very tired of how slow my implementation was. Now, my Python implementation was never especially well optimized and it had many additional functions that were in place for the project. The project was on unsupervised learning and I do not think it is quite ready for prime time so I won't go into detail here but I plan to keep working on it. Anyway, it was comically slow so I decided to significantly optimize it in both Python as well as c++, a language I did not know as of December 31st, call it a New Year's Resolution I guess. I still don't know it but I think I made some really great progress in this particular area so I'm here to present the results.

If I had to summarize what I did to optimize everything, it was put everything in arrays instead of that stupid class and don't use functions, do the logic in the single for loop iterating time. Also maybe avoid for loops in general, they're really quite slow. I don't actually have much to say other than I recreated the exact conditions of the original paper and the program, well the actual neuron interacting, runs in about 200 milliseconds. The initialization takes a fair bit longer but that's a one time hit so I don't really care and I can optimize that if I want. I actually finished optimizing the Python code after the c++ code because I just assumed that the Python code would always be comically slow. To be fair, it probably would be if I greatly increased the number of neurons but 1000 neurons in faster than real time is enough for plenty of projects but not all of them so I don't regret using doing the c++. I will publish my code but it is worth linking this which is an even more faithful recreation of the code and is faster. However, I think there is a bug in it because when I tried to graph the voltage over time I got a substantially different output than the izh paper. I don't want to knock the creator of that code, it's quite possible that my method of trying to take their output and turn it into a graph was just wrong but maybe not. Either way, the code really helped me optimize my own, I really didn't appreciate just how slow my code was until seeing their performance. The picture at the start is taken from my implementation. The below image is a recreation of figure 3 in the izh paper.

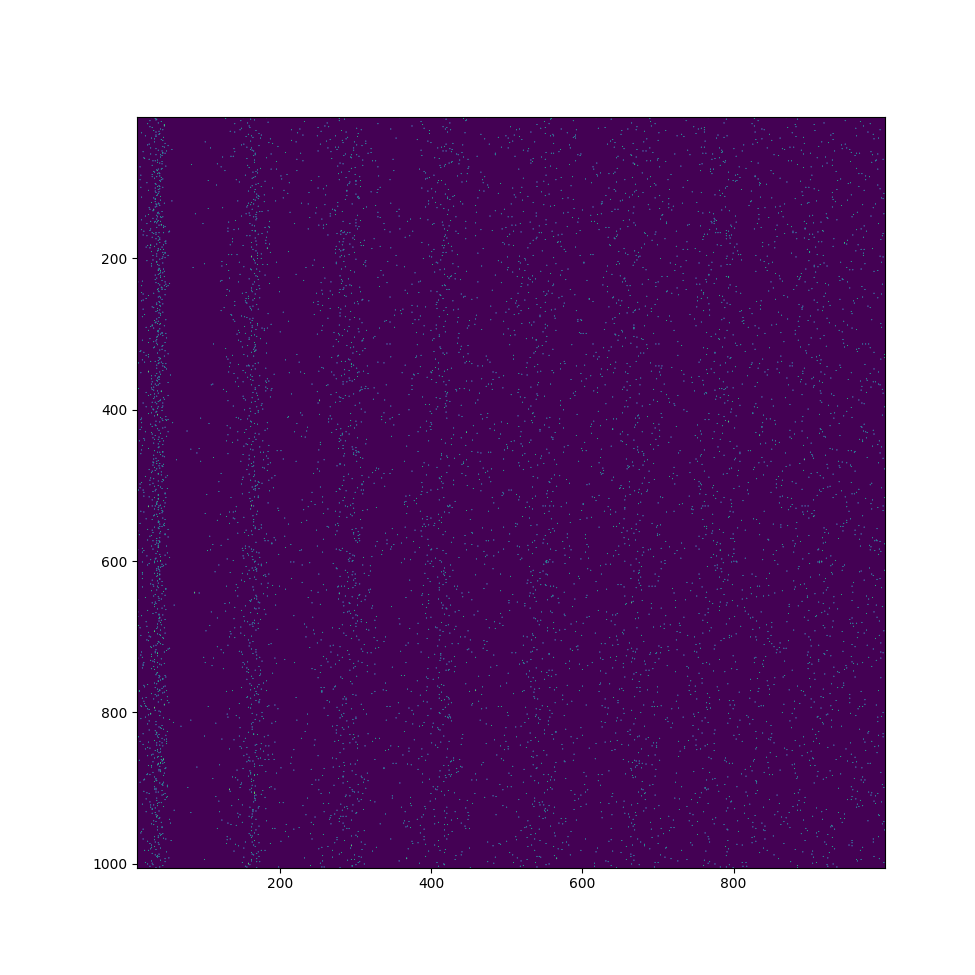
The c++ version, well technically the cuda version because everything is running on the gpu, is still a work in progress but it has allowed me to simulate more neurons than ever in almost real time. As it stands, I can simulate 2^20 (just over a million) neurons each with ~1000 synapses in about 1/10th real speed. I wrote everything to run on the gpu in hopes of it being massively parallel. It should be but I don't think it is because I am facing approximately linear slowdown. I'm probably just making a stupid mistake but I really don't have any experience with cuda or c++ so I can't fix it. Anyway, getting that many neurons just to fit in the gpu was a bit of a challenge in and of itself. My gpu has 8gb of ram and I was literally running out of space before I optimized everything. Now a clever man probably could have just used the system ram and faced a negligible slow down, but I didn't and I'll explain how I got everything to fit. The biggest thing is the matrix that stores the weights. In the Python implementation, the synaptic current is calculated by doing a matrix multiplication on the array storing the information of which neurons have just fired. There are two things wrong with this method. First, it kind of assumes that each neuron is, or has the potential to be, connected to every other neuron. As such, the size of the matrix grows with the square of the number of neurons. The second comes when you try and fix the first. The easiest thing would be to just set a bunch of the entries to zero and carry on doing a matrix multiplication. This works but then you're wasting a lot of space storing a bunch of zeros. In c++ (I'm still new, don't judge me if I say something dumb) you have reserve memory and you list a number of elements and a size. So to store a matrix as described above, even if it's mostly zeros, you would request enough space to store n^2 floats. This is fine for a few thousand but I would completely run out of space for a million neurons. To fix this, I changed the way the synaptic weights are stored and used to calculate the synaptic current. Instead of an n by n matrix, there are two n by k matrices. The index for n of course denoted the pre synaptic neuron index, the value stored at [n][k] in the first matrix gave the post synaptic neuron index and the value stored at [n][k] in the second matrix gives the synaptic weight. In cases were n >> k such as my own, this gives significant space savings and grows linearly with number of neurons rather than quadratically.

That is far and away the biggest change but something else of note is that I significantly decreased the size requirement to store the fit parameters. In the izh paper, he only uses excitatory and inhibitory neurons. As such, to store all the unique values of the fit parameters, you don't need a 4 by n matrix of floats, you only need an array of length n floats and a second array storing a boolean indicating if a neuron is excitatory or inhibitory. The first array will store the deviation of the fit parameters from the template values and the second array determines which of the two templates to pick from. This could be expanded to many different types of neurons although it won't ever be quite as good as having full independent values stored for each of the four fit parameters. Another minor change I made was the method of injecting random noise into the current of the neurons. My initial thought was to simply call a random number generator once for each neuron. Sense this was supposed to be in parallel, I didn't expect much slow down. This was incorrect and thus I looked for an alternative method. What I currently have is an array of pre-generated random numbers and each neuron picks an element from that array and picks a different one each timestep. This isn't quite as good as truly random number generation, but it is about five times faster which I think is an acceptable trade off. Below is an image of the voltage over time for neurons simulated on the gpu, I think it's alright.

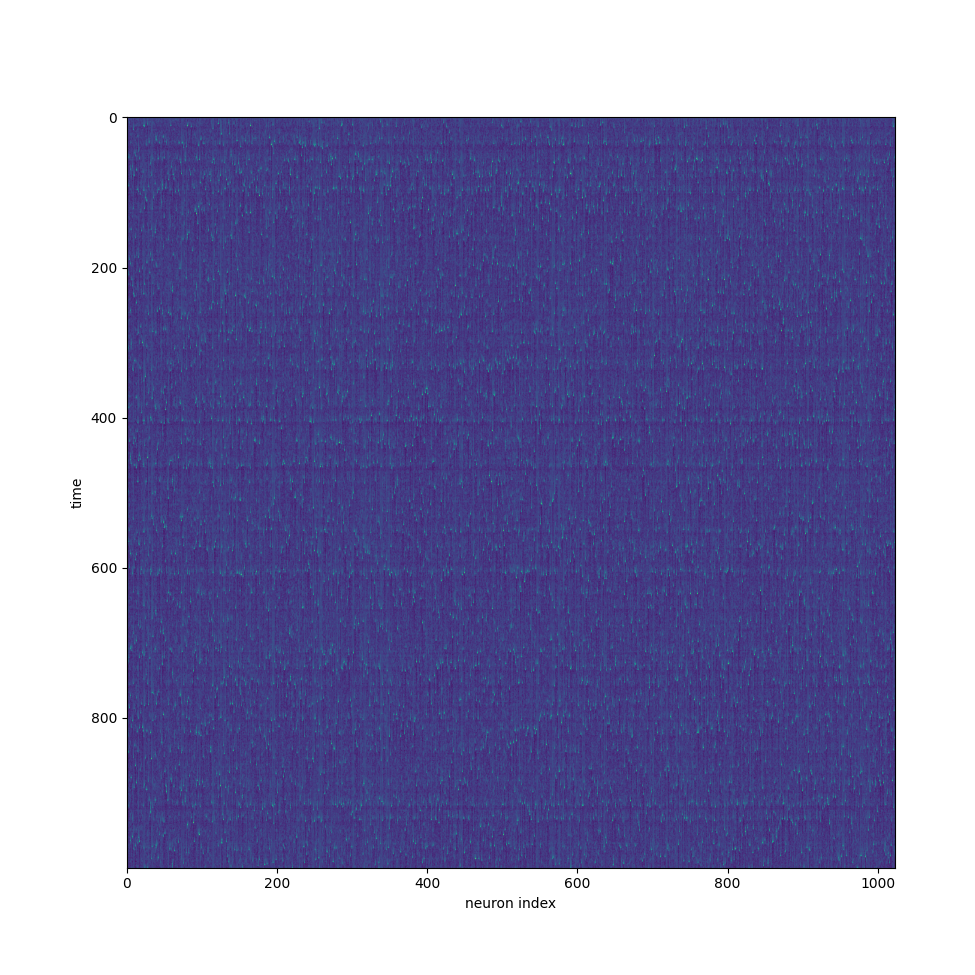
So what now? The most obvious thing is to just get it to run faster. A factor of 10 speed up is not actually that bad as far as it goes, I've already optimized my code to be thousands of times faster. Of course that really speaks to how poor my code was initially rather than how good it is now. I'm hoping that there really is one simple fix that gets away from my linear slowdown and everything just kind of works at a faster speed. I wouldn't be hugely surprised if I only had to change a few lines of code to get everything completely parallel, assuming that actually the issue. Other than that, the original goal was actually to get 10's of millions neurons because that's how many a mouse has. I'm not sure exactly why, it's not like we have mapped a mouse brain or anything so I couldn't upload a mouse brain into my computer. I guess it just seems like a nice benchmark. To get that many neurons I'm going to try and decrease the precision and/or the number of parameters used. I feel like 32 bit precision is a bit excessive but who knows. I really don't want to lose the accuracy of the model by dropping parameters but I would also be surprised if the level of accuracy in the Izhikevich is sufficient to simulate a whole mouse brain. Maybe it is but from what I can tell, many expect that there needs to be explicit modeling of the charge distribution dependent on position within the neuron. Also, I would be a little surprised if we could abstract away all the biochemistry involved in neurotransmitters (which I don't actually understand) in favor of just modeling the membrane potential. It is really convenient to ignore all those complexities but it probably isn't realistic or accurate for the whole brain. All that said, I also intend to do some interesting machine learning projects using all this and for that I don't strictly need any additional biological accuracy. Using what I already have or maybe even dropping it down to a leaky integrate and fire model or something is fine for that sort of application. Anyway here are the links to the Python and c++ versions.